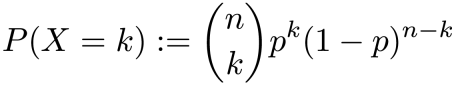Binomische Formeln
Die drei Basisgleichungen
$$
\begin{aligned}
(a+b)^2 &= a^2 +2ab + b^2 \\
(a-b)^2 &= a^2 -2ab + b^2 \\
(a+b)(a-b) &= a^2 - b^2
\end{aligned}
$$
Das Pascalsche Dreieck
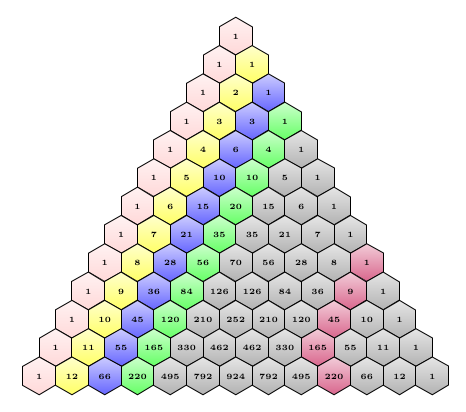
$$
\begin{aligned}
(a+b)^0 &= 1 \\
(a+b)^1 &= a+b \\
(a+b)^2 &= a^2 +2ab + b^2 \\
(a+b)^3 &= a^3 + 3a^2b+3ab^2+b^3 \\
(a+b)^4 &= a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 \\
(a+b)^5 &= a^5 +5a^4b +10a^3b^2+10a^2b^3 +5ab^4+b^5
\end{aligned}
$$
Die binomische Formel
Man wird sich unweigerlich die Frage stellen müssen, wie eine Lösung für
$$
(a+b)^n
$$
aussieht. Jetzt wird es etwas schwieriger. Wir führen den Binomialkoeffizienten ein:
$$
\binom{n}{k} = \frac{n!}{(n-k)!k!}
$$
Dann lautet die Lösung für unser Problem mit \(n \in \mathbb{N}\):
$$
(a+b)^n = \sum_{k=0}^n \binom{n}{k}a^{n-k}b^k
$$
Man bezeichnet den Ausdruck als binomische Formel. Oder:
$$
(a+b)^n = \binom{n}{0}a^n+\binom{n}{1}a^{n-1}b^1+\binom{n}{2}a^{n-2}b^2+\cdots+\binom{n}{k}a^{n-k}b^k+\cdots + \binom{n}{n}b^n
$$
Wir berechnen für \(n=6\):
$$
\begin{aligned}
(a+b)^6 &= \binom{6}{0}a^6 + \binom{6}{1}a^5b^1+\binom{6}{2}a^4b^2+\binom{6}{3}a^3b^3+\binom{6}{4}a^2b^4+\binom{6}{5}a^1b^5+\binom{6}{6}b^6 \\
& = a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6
\end{aligned}
$$